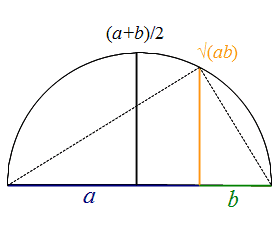均值不等式学习笔记

发表于 分类于

从平均数说起

我们都知道 nn 个数的平均数表示为：

a1+a2+a3+⋯ann\frac{a_1+a_2+a_3+\cdots a_n}{n}

这种最常见的平均数被称为“算术平均数”（Arithmetic Mean）。还有一种常用的平均数为“几何平均数”（Geometric Mean），计算公式如下：

a1a2a3⋯ann\sqrt[n]{a_1 a_2 a_3\cdots a_n}

其几何意义为：考虑一个 nn 维“长方体”，各边长度用 aa 数组表示，则几何平均数为“与其体积相等的 nn 维正方体的边长”。

几何平均数在金融领域也十分常用，比如：初始股票有 100100 元，第一个月增长了 100%100\% 至 200200 元，第二个月跌了 50%50\% 回到 100100 元。现在计算平均增长率，如果使用算术平均数，则计算得 100%+(−50%)2=25%\frac{100\%+(-50\%)}{2}=25\%。

但通过常识我们知道答案应该为 00。朴素的计算方法为：假设平均增长率为 rr，则需要满足 (1+r)(1+r)=(1+100%)(1−50%)(1+r)(1+r)=(1+100\%)(1-50\%)。此时的 rr 才是需要求的平均增长率。可以发现，这个式子事实上就是在求 (1+100%)(1+100\%) 和 (1−50%)(1-50\%) 的几何平均数。

回到数学领域。事实上，这两种平均数是有严格的大小关系的，即均值不等式。

均值不等式

均值不等式（AM-GM Inequality）是数学中非常常用的一个公式，表示为：

a1+a2+a3+⋯ann≥a1a2a3⋯ann\frac{a_1+a_2+a_3+\cdots a_n}{n}\ge\sqrt[n]{a_1 a_2 a_3\cdots a_n}

即，nn 个数的算数平均值大于等于几何平均值。该不等式成立的条件为这 nn 个数是非负数。不等式取等的充分必要条件为这 nn 个数全部相等。

证明

证明有很多种，这里就拿最常见的一种证明讲解。

首先考虑只有两个数的情况。此时的证明比较容易：

(x−y)2≥0x2+y2−2xy≥0x2+y2≥2xy(x-y)^2\ge 0\\ x^2+y^2-2xy\ge 0\\ x^2+y^2\ge 2xy

令 x=a1,y=a2x=\sqrt{a_1},y=\sqrt{a_2}，则有：

a1+a2≥2a1a2a1+a22≥a1a2a_1+a_2\ge 2\sqrt{a_1 a_2}\\ \frac{a_1+a_2}{2}\ge\sqrt{a_1 a_2}

于是两个数的均值不等式得证。

接下来，推广到 n=2kn=2^k 时的证明。使用数学归纳法：

假设均值不等式在 n=kn=k 时成立，我们证明其在 n=2kn=2k 时成立：

a1+a2+a3+⋯+a2k2k≥a1a2a3⋯a2k2k\frac{a_1+a_2+a_3+\cdots+a_{2k}}{2k}\ge\sqrt[2k]{a_1 a_2 a_3\cdots a_{2k}}

⇔12(a1+a2+⋯+akk+ak+1+ak+2+⋯+a2kk)≥a1a2⋯akkak+1ak+2⋯a2kk\Leftrightarrow\frac{1}{2}(\frac{a_1+a_2+\cdots+a_k}{k}+\frac{a_{k+1}+a_{k+2}+\cdots+a_{2k}}{k})\ge\sqrt{\sqrt[k]{a_1 a_2\cdots a_{k}}\sqrt[k]{a_{k+1}a_{k+2}\cdots a_{2k}}}

设 x1=a1+a2+⋯+akk,x2=ak+1+ak+2+⋯+a2kk,y1=a1a2⋯akk,y2=ak+1ak+2⋯a2kkx_1=\frac{a_1+a_2+\cdots+a_k}{k},x_2=\frac{a_{k+1}+a_{k+2}+\cdots+a_{2k}}{k},y_1=\sqrt[k]{a_1 a_2\cdots a_{k}},y_2=\sqrt[k]{a_{k+1}a_{k+2}\cdots a_{2k}}，则由于假设 n=kn=k 时成立，所以 x1≥y1,x2≥y2x_1\ge y_1,x_2\ge y_2。又因为均值不等式在 n=2n=2 时成立，所以：

12(x1+x2)≥12(y1+y2)≥y1y2\frac{1}{2}(x_1+x_2)\ge\frac{1}{2}(y_1+y_2)\ge \sqrt{y_1 y_2}

由于 n=2n=2 时成立，所以可以推出 n=4,8,16⋯n=4,8,16\cdots 时也成立。故 n=2kn=2^k 时成立。

然后我们考虑倒序证明。我们证明：若均值不等式在 n=kn=k 时成立，则在 n=k−1n=k-1 时也成立。这个证明就比较容易了：

设这 k−1k-1 个数的算术平均值为 AA，则加入元素 AA 后形成的 kk 个数的数组算术平均值不变。由于在 n=kn=k 时成立，所以：

A≥a1a2⋯ak−1AkA\ge\sqrt[k]{a_1 a_2\cdots a_{k-1}A}

两边同时取 kk 次方，得：

Ak≥a1a2⋯ak−1AAk−1≥a1a2⋯ak−1A^k\ge a_1 a_2\cdots a_{k-1} A\\ A^{k-1}\ge a_1 a_2\cdots a_{k-1}

再同时取 k−1k-1 次根，得：A≥a1a2⋯ak−1k−1A\ge\sqrt[k-1]{a_1 a_2\cdots a_{k-1}}

于是得证。由于对于每个 nn 都存在某个 kk 使得 n≤2kn\le 2^k，所以可以从 2k2^k 一步步倒推，所以均值不等式对于任意 nn 成立。

对于两个数的均值不等式，还有一个巧妙的无字证明如下图：

由相似或勾股定理可以得出，黄线的长度即为 a,ba,b 的几何平均数。

应用

在应用上，有两个非常常用的转化，这里先写出来以省略后面的推导篇幅。

a1+a2+⋯an≥na1a2⋯anna1a2⋯an≤(a1+a2+⋯ann)na_1+a_2+\cdots a_n\ge n\sqrt[n]{a_1 a_2\cdots a_n}\\ a_1 a_2\cdots a_n\le (\frac{a_1+a_2+\cdots a_n}{n})^n

即：nn 个数的和大于等于 nn 倍几何平均；nn 个数的积小于等于算术平均的 nn 次方。证明显然，只是将均值不等式移了一下项。

问题一：证明对于周长固定的矩形，正方形的面积最大。

设周长为 CC，长宽为 a,ba,b，则有 a+b=C/2a+b=C/2。面积为 abab。由转化二可知，ab≤(a+b2)2=(C4)2ab\le(\frac{a+b}{2})^2=(\frac{C}{4})^2，因此面积 abab 最大不超过 (C4)2(\frac{C}{4})^2。由取等条件可知，ab=(C4)2ab=(\frac{C}{4})^2 当且仅当 a=ba=b，即为正方形。

问题二：某工厂要制造一个无盖的圆柱形桶，要求容积为 32π\frac{3}{2}\pi 立方米。底面的金属每平方米 33 元，侧面的每平方米 22 元。求最小造价以及方案。

设底面半径为 rr，高为 hh，则要求 πr2h=32π\pi r^2h=\frac{3}{2}\pi，即 r2h=32r^2h=\frac{3}{2}。此时的花费为 πr2⋅3+2πrh⋅2\pi r^2\cdot 3+2\pi rh\cdot 2。由均值不等式的转化一：

πr2⋅3+2πrh⋅2=πr2⋅3+2πrh+2πrh≥3πr2⋅3⋅2πrh⋅2πrh3=3π12r4h23=3π12(r2h)23=9π\begin{aligned} \pi r^2\cdot 3+2\pi rh\cdot 2&=\pi r^2\cdot 3+2\pi rh+2\pi rh\\ &\ge3\sqrt[3]{\pi r^2\cdot 3\cdot 2\pi rh\cdot 2\pi rh}\\ &=3\pi\sqrt[3]{12r^4h^2}\\ &=3\pi\sqrt[3]{12(r^2h)^2}\\ &=9\pi \end{aligned}

由取等条件可知，当 πr2⋅3=2πrh\pi r^2\cdot 3=2\pi rh 时花费最小，即 h=32rh=\frac{3}{2}r。

这个不等式的推导涉及到“拆项”的技巧，即第一行中把 2πrh⋅22\pi rh\cdot 2 拆成 2πrh+2πrh2\pi rh+2\pi rh。仔细观察上面的过程可以发现，均值不等式实际上将加法转换为了乘法。虽然是否拆项在加法上没有区别，但转化到乘法就会导致次数的不同。此处是为了凑 r4h2r^4h^2（因为给定 rhr^h 为常数）。

例题

题目传送门

题意：一个小球下落时间为 Ag\frac{A}{\sqrt{g}}，初始时 g=1g=1，每次可以花费 BB 的时间将 gg 增加 11，问最小总时间。

考虑答案关于 gg 的函数 f(g)=Ag+B(g−1)f(g)=\frac{A}{\sqrt{g}}+B(g-1)，由于最小值与常数无关，所以可以看成 f(g)=Ag+Bgf(g)=\frac{A}{\sqrt{g}}+Bg，则由均值不等式：

f(g)=Ag+Bg=A2g+A2g+Bg≥3A2B43\begin{aligned} f(g)&=\frac{A}{\sqrt{g}}+Bg\\ &=\frac{A}{2\sqrt{g}}+\frac{A}{2\sqrt{g}}+Bg\\ &\ge 3\sqrt[3]{\frac{A^2B}{4}} \end{aligned}

由此可知函数最小值不会小于 3A2B433\sqrt[3]{\frac{A^2B}{4}}，取等条件为 A2g=Bg\frac{A}{2\sqrt{g}}=Bg，即 g=(A2B)23g=(\frac{A}{2B})^\frac{2}{3}。

By EternalAlexander

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <bits/stdc++.h>
const long double eps = 1e-10;
using ldb = long double;
using ll = long long;
ldb a,b;
long double calc(long double x) {
    return x * b + (long double) a / std::sqrt(1 + x);
}

int main() {
    std::cin >> a >> b;
    long double x = pow( a / (2 * b) , 2.0 / 3 ) - 1;
    ll x1 = x;
    long double ans = a;
    for (ll p = x1 - 10; p <= x1 + 10; ++ p) ans = std::min(ans,calc(p));
    printf("%.10Lf",ans);
    return 0;
}