题意:有一个无向图,点有点权。定义两个节点“可达”当且仅当这两个节点的最短路不超过 k + 1 k+1 k + 1 { a , b , c , d } \{a,b,c,d\} { a , b , c , d } 1 ↔ a ↔ b ↔ c ↔ d ↔ 1 1\leftrightarrow a\leftrightarrow b\leftrightarrow c\leftrightarrow d\leftrightarrow 1 1 ↔ a ↔ b ↔ c ↔ d ↔ 1 n ≤ 2500 n\le 2500 n ≤ 2 5 0 0
首先跑 n n n b , c b,c b , c a , d a,d a , d 1 ↔ a ↔ b 1\leftrightarrow a\leftrightarrow b 1 ↔ a ↔ b c ↔ d ↔ 1 c\leftrightarrow d\leftrightarrow 1 c ↔ d ↔ 1 x x x 1 ↔ y ↔ x 1\leftrightarrow y\leftrightarrow x 1 ↔ y ↔ x y y y y y y b , c b,c b , c v [ a ] v[a] v [ a ] 1 ↔ a ↔ b 1\leftrightarrow a\leftrightarrow b 1 ↔ a ↔ b v [ d ] v[d] v [ d ] 1 ↔ d ↔ c 1\leftrightarrow d\leftrightarrow c 1 ↔ d ↔ c v [ a ] v[a] v [ a ] a = c a=c a = c v [ a ] , v [ d ] v[a],v[d] v [ a ] , v [ d ] a = d a=d a = d b , c b,c b , c 9 9 9
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 #include <bits/stdc++.h> using namespace std;#define int long long int v[2510 ];vector<int > a[2510 ]; bool e[2510 ][2510 ];vector<int > to[2510 ]; bool vis[2510 ];signed main () int n,m,kk; scanf ("%lld%lld%lld" ,&n,&m,&kk); for (int i=2 ;i<=n;i++) scanf ("%lld" ,&v[i]); for (int i=1 ;i<=m;i++) { int x,y; scanf ("%lld%lld" ,&x,&y); a[x].push_back (y); a[y].push_back (x); } for (int i=1 ;i<=n;i++) { memset (vis,0 ,sizeof queue<pair<int ,int > > q; q.push ({i,0 }); while (!q.empty ()) { auto u=q.front ();q.pop (); if (u.second>kk+1 ) break ; if (vis[u.first]) continue ; vis[u.first]=1 ,e[i][u.first]=1 ; for (int v:a[u.first]) if (!vis[v]) q.push ({v,u.second+1 }); } } for (int i=2 ;i<=n;i++) { for (int j=2 ;j<=n;j++) if (i!=j&&e[i][j]&&e[1 ][j]) to[i].push_back (j); sort (to[i].begin (),to[i].end (),[&](int x,int y) { return v[x]>v[y]; }); } int ans=0 ; for (int i=2 ;i<=n;i++) for (int j=i+1 ;j<=n;j++) { if (!e[i][j]) continue ; for (int k=0 ;k<min (3ll ,(int )to[i].size ());k++) for (int l=0 ;l<min (3ll ,(int )to[j].size ());l++) if (to[i][k]!=j&&to[j][l]!=i&&to[i][k]!=to[j][l]) ans=max (ans,v[i]+v[j]+v[to[i][k]]+v[to[j][l]]); } printf ("%lld\n" ,ans); return 0 ; }
题意:给你两个数组 a ( n ) , b ( m ) a(n),b(m) a ( n ) , b ( m ) l 1 , r 1 , l 2 , r 2 l_1,r_1,l_2,r_2 l 1 , r 1 , l 2 , r 2 i ∈ [ l 1 , r 1 ] i\in[l_1,r_1] i ∈ [ l 1 , r 1 ] j ∈ [ l 2 , r 2 ] j\in[l_2,r_2] j ∈ [ l 2 , r 2 ] a i ⋅ b j a_i\cdot b_j a i ⋅ b j n , m , q ≤ 1 0 5 n,m,q\le 10^5 n , m , q ≤ 1 0 5
容易发现,此题可以直接分类讨论正负后贪心。如果第一个人选正数,那么第二个人一定会选能选的最小的数。如果第二个人能选到负数则一定会选,此时第一个人选的正数越小越好,否则越大越好。如果第一个人选负数,那么第二个人一定会选最大值。如果第二个人能选到正数则一定会选,此时第一个人选的越大(即越接近 0 0 0
实现上,可以使用线段树维护两个序列的正数最大值、最小值和负数最大值、最小值,每次区间询问合并区间信息即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 #include <bits/stdc++.h> using namespace std;int a[2 ][100010 ];#define mid (t[now].l+t[now].r)/2 #define lson now*2 #define rson now*2+1 struct node { int l,r,maxp,minp,maxn,minn; bool havep,haven; node ():havep (0 ),haven (0 ){} }; struct segtree { node t[400010 ]; node merge (node x,node y) { node res; res.l=x.l,res.r=y.r; res.havep=(x.havep||y.havep); res.haven=(x.haven||y.haven); if (x.havep&&y.havep) { res.maxp=max (x.maxp,y.maxp); res.minp=min (x.minp,y.minp); } else if (x.havep||y.havep) { res.maxp=x.maxp*x.havep+y.maxp*y.havep; res.minp=x.minp*x.havep+y.minp*y.havep; } if (x.haven&&y.haven) { res.maxn=max (x.maxn,y.maxn); res.minn=min (x.minn,y.minn); } else if (x.haven||y.haven) { res.maxn=x.maxn*x.haven+y.maxn*y.haven; res.minn=x.minn*x.haven+y.minn*y.haven; } return res; } void build (int now,int l,int r,bool flag) t[now].l=l,t[now].r=r; if (l==r) { if (a[flag][l]>=0 ) { t[now].havep=1 ; t[now].maxp=t[now].minp=a[flag][l]; } else { t[now].haven=1 ; t[now].maxn=t[now].minn=a[flag][l]; } return ; } build (lson,l,mid,flag); build (rson,mid+1 ,r,flag); t[now]=merge (t[lson],t[rson]); } node query (int now,int l,int r) { if (l<=t[now].l&&r>=t[now].r) return t[now]; node res; if (l<=mid) res=merge (res,query (lson,l,r)); if (r>mid) res=merge (res,query (rson,l,r)); return res; } } T1,T2; void chkmax (long long &x,long long y) int main () int n,m,q; scanf ("%d%d%d" ,&n,&m,&q); for (int i=1 ;i<=n;i++) scanf ("%d" ,&a[0 ][i]); for (int i=1 ;i<=m;i++) scanf ("%d" ,&a[1 ][i]); T1.build (1 ,1 ,n,0 ); T2.build (1 ,1 ,m,1 ); while (q--) { int l1,r1,l2,r2; scanf ("%d%d%d%d" ,&l1,&r1,&l2,&r2); node A=T1.query (1 ,l1,r1); node B=T2.query (1 ,l2,r2); long long ans=-1e18 ; if (A.havep) { if (B.haven) chkmax (ans,1ll *A.minp*B.minn); else chkmax (ans,1ll *A.maxp*B.minp); } if (A.haven) { if (B.havep) chkmax (ans,1ll *A.maxn*B.maxp); else chkmax (ans,1ll *A.minn*B.maxn); } printf ("%lld\n" ,ans); } return 0 ; }
题意:有一张简单的有向图(不保证连通),每条边有可用和不可用两种状态,初始每条边都可用。定义一个图是合法的,当且仅当:
从每个点开始都存在一个合适的移动方式使得能够无限移动下去。
每个点有且仅有一条出边。
你需要进行 q q q
给出 u , v u,v u , v u → v u\to v u → v
给出 u u u x → u x\to u x → u
给出 u , v u,v u , v u → v u\to v u → v
给出 u u u x → u x\to u x → u
每次操作后回答这张图是否合法。n , m , q ≤ 5 × 1 0 5 n,m,q\le 5\times 10^5 n , m , q ≤ 5 × 1 0 5
可以发现,合法的限制一是没有用的。因为如果满足了限制二,该有向图一定为一个基环内向树森林,于是每个节点必然可以通向一个环。可以通过反证法简单地证明:如果存在某个点不能无限移动下去,设它的终点为 x x x x x x
于是问题转化为每次操作后判断是否每个点的出度均为 1 1 1
我们考虑通过哈希来维护这一过程。我们给每个点赋一个随机权值,维护当前每条边起点的权值和 n o w s u m nowsum n o w s u m a l l all a l l n o w s u m = a l l nowsum=all n o w s u m = a l l
对于暴力连边和断边的操作,可以直接在 n o w s u m nowsum n o w s u m n o w i now_i n o w i i i i s u m i sum_i s u m i i i i
暴力连断边:根据定义,n o w s u m nowsum n o w s u m x x x n o w y now_y n o w y x x x
删点、恢复点:使用 n o w x now_x n o w x s u m x sum_x s u m x n o w s u m nowsum n o w s u m
可以感性理解成势能和动能的转化:n o w i now_i n o w i n o w s u m nowsum n o w s u m
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 #include <bits/stdc++.h> using namespace std;long long a[500010 ],sum[500010 ],now[500010 ];signed main () srand (time (0 )); int n,m,q; scanf ("%d%d" ,&n,&m); long long nowsum=0 ,all=0 ; for (int i=1 ;i<=n;i++) a[i]=rand (),all+=a[i]; for (int i=1 ;i<=m;i++) { int x,y; scanf ("%d%d" ,&x,&y); sum[y]+=a[x],now[y]+=a[x],nowsum+=a[x]; } scanf ("%d" ,&q); while (q--) { int op,x,y; scanf ("%d%d" ,&op,&x); if (op==1 ||op==3 ) scanf ("%d" ,&y); if (op==1 ) now[y]-=a[x],nowsum-=a[x]; else if (op==2 ) nowsum-=now[x],now[x]=0 ; else if (op==3 ) now[y]+=a[x],nowsum+=a[x]; else nowsum+=sum[x]-now[x],now[x]=sum[x]; if (nowsum==all) puts ("YES" ); else puts ("NO" ); } return 0 ; }
题意:给你一个树,第 i i i v i ( > 0 ) v_i(>0) v i ( > 0 ) k k k s , t s,t s , t s s s t t t s → c 1 → c 2 → ⋯ → t s\to c_1\to c_2\to\cdots\to t s → c 1 → c 2 → ⋯ → t min c { s + ∑ c + t } \min\limits_c\{s+\sum c+t\} c min { s + ∑ c + t } n , q ≤ 2 × 1 0 5 , k ≤ 3 n,q\le 2\times 10^5,k\le 3 n , q ≤ 2 × 1 0 5 , k ≤ 3
首先考虑最简单的 k = 1 k=1 k = 1
对于 k = 2 k=2 k = 2 O ( n ) O(n) O ( n )
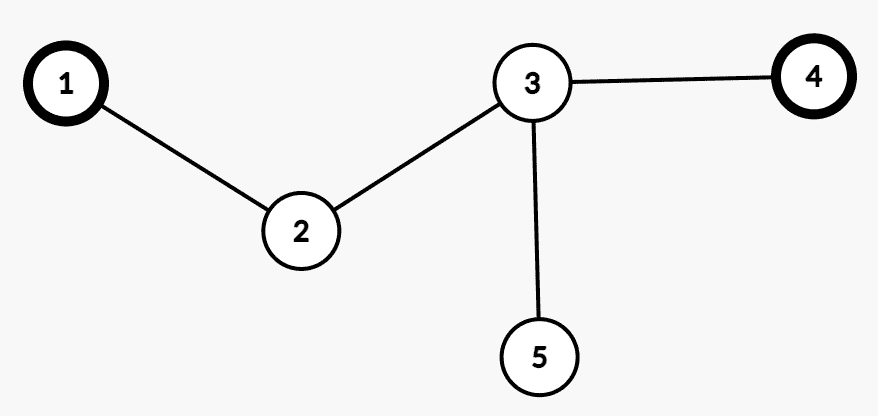
我们可以从 2 2 2 5 5 5 4 4 4 2 2 2 4 4 4
对于 k = 3 k=3 k = 3
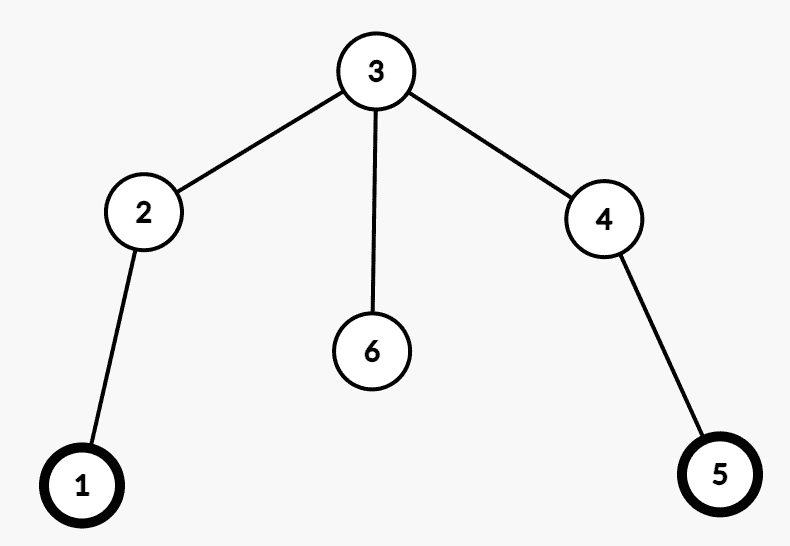
此时如果点 6 6 6 2 , 3 , 4 2,3,4 2 , 3 , 4 1 → 6 → 5 1\to 6\to 5 1 → 6 → 5 k = 2 k=2 k = 2
然后我们考虑扩展 DP 状态:定义 f [ i ] [ j ∈ { 0 , 1 , 2 } ] f[i][j\in\{0,1,2\}] f [ i ] [ j ∈ { 0 , 1 , 2 } ] i i i i i i j j j
f [ i ] [ 0 ] f[i][0] f [ i ] [ 0 ] i i i i − 1 i-1 i − 1 i − 1 i-1 i − 1 1 1 1 i − 1 i-1 i − 1 2 2 2 f [ i ] [ 0 ] = min ( f [ i − 1 ] [ 0 ] + v i , f [ i − 1 ] [ 1 ] + v i , f [ i − 1 ] [ 2 ] + v i ) f[i][0]=\min(f[i-1][0]+v_i,f[i-1][1]+v_i,f[i-1][2]+v_i) f [ i ] [ 0 ] = min ( f [ i − 1 ] [ 0 ] + v i , f [ i − 1 ] [ 1 ] + v i , f [ i − 1 ] [ 2 ] + v i )
f [ i ] [ 1 ] f[i][1] f [ i ] [ 1 ] i i i 1 1 1
此时当前所在的位置有 i − 1 , a , b , i + 1 i-1,a,b,i+1 i − 1 , a , b , i + 1 i − 1 i-1 i − 1 f [ i − 1 ] [ 0 ] f[i-1][0] f [ i − 1 ] [ 0 ] c c c i − 2 i-2 i − 2 i − 1 i-1 i − 1 1 1 1 i − 1 i-1 i − 1 i − 1 → a i-1\to a i − 1 → a i − 1 i-1 i − 1 i − 1 → a i-1\to a i − 1 → a f [ i ] [ 1 ] = min ( f [ i − 1 ] [ 0 ] , f [ i − 1 ] [ 1 ] + m n i ) f[i][1]=\min(f[i-1][0],f[i-1][1]+mn_i) f [ i ] [ 1 ] = min ( f [ i − 1 ] [ 0 ] , f [ i − 1 ] [ 1 ] + m n i ) m n i mn_i m n i i i i i i i m n mn m n
f [ i ] [ 2 ] f[i][2] f [ i ] [ 2 ] c c c i − 2 i-2 i − 2 i − 1 i-1 i − 1 1 1 1 f [ i − 1 ] [ 1 ] f[i-1][1] f [ i − 1 ] [ 1 ] f [ i ] [ 2 ] = f [ i − 1 ] [ 1 ] f[i][2]=f[i-1][1] f [ i ] [ 2 ] = f [ i − 1 ] [ 1 ]
结合以上分析,我们得到了如下的 DP 方程:
f [ i ] [ 0 ] = min ( f [ i − 1 ] [ 0 ] + v i , f [ i − 1 ] [ 1 ] + v i , f [ i − 1 ] [ 2 ] + v i ) f [ i ] [ 1 ] = min ( f [ i − 1 ] [ 0 ] , f [ i − 1 ] [ 1 ] + m n i ) f [ i ] [ 2 ] = min ( f [ i − 1 ] [ 1 ] ) \begin{aligned}
f[i][0]&=\min(f[i-1][0]+v_i,f[i-1][1]+v_i,f[i-1][2]+v_i)\\
f[i][1]&=\min(f[i-1][0],f[i-1][1]+mn_i)\\
f[i][2]&=\min(f[i-1][1])
\end{aligned}
f [ i ] [ 0 ] f [ i ] [ 1 ] f [ i ] [ 2 ] = min ( f [ i − 1 ] [ 0 ] + v i , f [ i − 1 ] [ 1 ] + v i , f [ i − 1 ] [ 2 ] + v i ) = min ( f [ i − 1 ] [ 0 ] , f [ i − 1 ] [ 1 ] + m n i ) = min ( f [ i − 1 ] [ 1 ] )
(最后一个为了统一格式也用 min \min min f [ i ] f[i] f [ i ] f [ i − 1 ] f[i-1] f [ i − 1 ] i i i [ A ⋅ B ] i , j = min k { A i , k + B k , j } [A\cdot B]_{i,j}=\min\limits_k\{A_{i,k}+B_{k,j}\} [ A ⋅ B ] i , j = k min { A i , k + B k , j }
( A ⋅ ( B ⋅ C ) ) i , j = min k { A i , k + ( B ⋅ C ) k , j } = min k { A i , k + min p { B k , p + C p , j } } = min k { min p { A i , k + B k , p + C p , j } } = min p { min k { A i , k + B k , p + C p , j } } = min p { min k { A i , k + B k , p } + C p , j } = min p { ( A ⋅ B ) i , p + C p , j } = ( ( A ⋅ B ) ⋅ C ) i , j \begin{aligned}
(A\cdot (B\cdot C))_{i,j}&=\min\limits_k\{A_{i,k}+(B\cdot C)_{k,j}\}\\
&=\min\limits_k\left\{A_{i,k}+\min\limits_p\{B_{k,p}+C_{p,j}\}\right\}\\
&=\min\limits_k\left\{\min\limits_p\{A_{i,k}+B_{k,p}+C_{p,j}\}\right\}\\
&=\min\limits_p\left\{\min\limits_k\{A_{i,k}+B_{k,p}+C_{p,j}\}\right\}\\
&=\min\limits_p\left\{\min\limits_k\{A_{i,k}+B_{k,p}\}+C_{p,j}\right\}\\
&=\min\limits_p\{(A\cdot B)_{i,p}+C_{p,j}\}\\
&=((A\cdot B)\cdot C)_{i,j}
\end{aligned}
( A ⋅ ( B ⋅ C ) ) i , j = k min { A i , k + ( B ⋅ C ) k , j } = k min { A i , k + p min { B k , p + C p , j } } = k min { p min { A i , k + B k , p + C p , j } } = p min { k min { A i , k + B k , p + C p , j } } = p min { k min { A i , k + B k , p } + C p , j } = p min { ( A ⋅ B ) i , p + C p , j } = ( ( A ⋅ B ) ⋅ C ) i , j
这是一个经典的矩阵乘法的定义:内层相加,外层极值。于是,我们可以把 DP 转移转化为下面的矩阵乘法:
[ f [ i ] [ 0 ] f [ i ] [ 1 ] f [ i ] [ 2 ] ] = [ f [ i − 1 ] [ 0 ] f [ i − 1 ] [ 1 ] f [ i − 1 ] [ 2 ] ] ⋅ [ v i 0 + ∞ v i m n i 0 v i + ∞ + ∞ ] \begin{bmatrix}
f[i][0] & f[i][1] & f[i][2]
\end{bmatrix}
=
\begin{bmatrix}
f[i-1][0] & f[i-1][1] & f[i-1][2]
\end{bmatrix}
\cdot
\begin{bmatrix}
v_i & 0 & +\infty\\
v_i & mn_i & 0\\
v_i & +\infty & +\infty
\end{bmatrix}
[ f [ i ] [ 0 ] f [ i ] [ 1 ] f [ i ] [ 2 ] ] = [ f [ i − 1 ] [ 0 ] f [ i − 1 ] [ 1 ] f [ i − 1 ] [ 2 ] ] ⋅ ⎣ ⎢ ⎡ v i v i v i 0 m n i + ∞ + ∞ 0 + ∞ ⎦ ⎥ ⎤
在 k = 2 k=2 k = 2
由于结合律,问题转化为求路径上每个节点的矩阵乘积。由于树上的路径可以分为向上的一段和向下的一段,我们考虑倍增求树上 ST 表。定义 g [ i ] [ j ] g[i][j] g [ i ] [ j ] i i i 2 j 2^j 2 j g g g h [ i ] [ j ] h[i][j] h [ i ] [ j ] g [ i ] [ j ] g[i][j] g [ i ] [ j ] s s s q n log ( n ) × k 3 qn\log(n)\times k^3 q n log ( n ) × k 3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 #include <bits/stdc++.h> using namespace std;#define int long long int n,q,k,v[200010 ];struct matrix { int n,a[3 ][3 ]; matrix operator *(matrix o) { matrix res; res.n=n; for (int i=0 ;i<n;i++) for (int j=0 ;j<n;j++) { res.a[i][j]=1e18 ; for (int k=0 ;k<n;k++) res.a[i][j]=min (res.a[i][j],a[i][k]+o.a[k][j]); } return res; } } f[200010 ][20 ],g[200010 ][20 ]; vector<int > e[200010 ]; int fa[200010 ][20 ],mn[200010 ],dep[200010 ];void dfs (int now,int father,int depth) fa[now][0 ]=father,dep[now]=depth; f[now][0 ].n=k; auto &t=f[now][0 ].a; for (int i=0 ;i<3 ;i++) t[i][0 ]=v[now]; t[0 ][1 ]=t[1 ][2 ]=0 ; t[1 ][1 ]=mn[now]; t[2 ][1 ]=t[0 ][2 ]=t[2 ][2 ]=1e18 ; if (k==2 ) t[1 ][1 ]=1e18 ; g[now][0 ]=f[now][0 ]; for (int to:e[now]) if (to!=father) dfs (to,now,depth+1 ); } int LCA (int x,int y) if (dep[x]<dep[y]) swap (x,y); for (int i=19 ;i>=0 ;i--) if (dep[fa[x][i]]>=dep[y]) x=fa[x][i]; if (x==y) return x; for (int i=19 ;i>=0 ;i--) if (fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i]; return fa[x][0 ]; } signed main () memset (mn,0x3f ,sizeof scanf ("%lld%lld%lld" ,&n,&q,&k); matrix init; init.n=k; for (int i=0 ;i<k;i++) for (int j=0 ;j<k;j++) init.a[i][j]=(i!=j)*1e18 ; for (int i=1 ;i<=n;i++) scanf ("%lld" ,&v[i]); for (int i=1 ;i<n;i++) { int x,y; scanf ("%lld%lld" ,&x,&y); e[x].push_back (y); e[y].push_back (x); mn[x]=min (mn[x],v[y]); mn[y]=min (mn[y],v[x]); } dfs (1 ,0 ,1 ); for (int x=0 ;x<=19 ;x++) f[0 ][x]=g[0 ][x]=init; for (int j=1 ;j<=19 ;j++) for (int i=1 ;i<=n;i++) { fa[i][j]=fa[fa[i][j-1 ]][j-1 ]; f[i][j]=f[i][j-1 ]*f[fa[i][j-1 ]][j-1 ]; g[i][j]=g[fa[i][j-1 ]][j-1 ]*g[i][j-1 ]; } while (q--) { int s,t; scanf ("%lld%lld" ,&s,&t); int lca=LCA (s,t),x=v[s]; s=fa[s][0 ]; matrix tmp1=init,tmp2=init; for (int i=19 ;i>=0 &&s;i--) if (dep[fa[s][i]]+1 >=dep[lca]) tmp1=tmp1*f[s][i],s=fa[s][i]; for (int i=19 ;i>=0 &&t;i--) if (dep[fa[t][i]]>=dep[lca]) tmp2=g[t][i]*tmp2,t=fa[t][i]; matrix ans=tmp1*tmp2; printf ("%lld\n" ,ans.a[0 ][0 ]+x); } return 0 ; }