EDU-CFR-138解题报告

发表于 分类于

比赛传送门

A. Cowardly Rooks

题意：有一个 n×nn\times n 的棋盘，有 mm 个位置上有车，保证互不攻击。问是否能将一个车移动一次使得仍然互不攻击。

稍加思考可得，如果 m≠nm\ne n，一定可以，否则一定不可以。因为如果 m<nm<n，则一定有一列是空着的，随便选一辆车移动到该列即可。如果 m=nm=n，易证一定不可以。

By caoxuanming

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include<bits/stdc++.h>
using namespace std;
signed main() {
    int t;
    cin>>t;
    while(t--) {
        int n,m,x,y;
        cin>>n>>m;
        for(int i=1;i<=m;i++)
            cin>>x>>y;
        if(n==m) cout<<"NO"<<endl;
        else cout<<"YES"<<endl;
    }
    return 0;
}

B. Death’s Blessing

题意：有 nn 个怪物排成一排，每个怪物有 ai,bia_i,b_i 两个权值。杀掉一个怪物需要花费 aia_i 的代价，同时会导致与其相邻的怪物的 aa 增加 bib_i。杀掉后左右两边变成相邻的。求全部杀完的最小代价。

我们从贡献的角度考虑。显然每个怪物的 aia_i 都会且仅会给答案造成 aia_i 的贡献，所以可以不用考虑。对于 bib_i，只有杀掉的时候会产生贡献，所以只会贡献一“次”，而每次可以造成 0/1/2 倍的贡献（根据邻居数量）。显然，0 倍贡献只有最后一个怪物可以达到，而其他的怪物要么 1 倍要么 2 倍。此时显然每个其他怪物都用 1 倍更优，而这种方案是一定能够达到的：只需要从两边依次取到最后一个怪物的位置即可。所以只需要让 bb 最大的怪物造成 0 倍，其他造成 1 倍即可。

By caoxuanming

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<bits/stdc++.h>
using namespace std;
#define int long long
int a[200010],b[200010];
signed main() {
    int t;
    cin>>t;
    while(t--) {
        int n;
        cin>>n;
        for(int i=1;i<=n;i++)
            cin>>a[i];
        for(int i=1;i<=n;i++)
            cin>>b[i];
        int maxn=0,sum=0;
        for(int i=1;i<=n;i++) {
            maxn=max(maxn,b[i]);
            sum+=a[i]+b[i];
        }
        cout<<sum-maxn<<endl;
    }
    return 0;
}

C. Number Game

题意：有一个长度为 nn 的序列 aa，进行 kk 次操作。第一次操作 Alice 可以删掉一个 ≤k\le k 的数并由 Bob 再删掉一个数（如果没有可以不删）；第二次操作 Alice 可以删掉一个 ≤k−1\le k-1 的数并由 Bob 再删掉一个数（如果没有可以不删），以此类推直到第 kk 次操作删掉一个 ≤1\le 1 的数。如果在某次操作中 Alice 无数可删则 Bob 赢，否则 Alice赢。问 Alice 能赢的最大的 kk。

显然 kk 不会超过 nn，于是从 11 到 nn 枚举 kk，每次模拟 kk 次操作即可。贪心地考虑，Alice 每次一定选能选的最大的数删（因为以后可能就没法删了），而 Bob 每次一定选最小的数删（最小的威胁最大，因为更容易被 Alice 删掉）。于是我们在排好序的数组上维护一个双指针即可。

By gyh20

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int t,n,m,a[1000002],A,B,R[1000002],stk[1000002],tp;
char s[1000002];
long long ans;
inline bool ck(re int x){
    int pos=n;
    while(a[pos]>x)--pos;
    for(re int i=1;i<=x;++i){
        while(a[pos]>x-i+1)--pos;
        if(pos<i)return 0;--pos;
    }return 1;
}
int main(){
    t=read();
    while(t--){
        n=read();ans=0;
        for(re int i=1;i<=n;++i)a[i]=read();sort(a+1,a+n+1);
        for(re int i=n;~i;--i)
            if(ck(i)){
                printf("%d\n",i);
                break;
            }
    }
}

D. Counting Arrays

题意：假设有一个序列 a1∼aka_1\sim a_k，我们可以以某种顺序依次删除这 kk 个元素，要求每次删除的数与“当前它所处的位置”互质。问有多少个长度在 [1,n][1,n]，值域在 [1,m][1,m] 的序列，满足有 ≥2\ge 2 种满足条件的删除方式。

首先，由于任何序列都存在一种平凡的满足条件的删除方式———每次都删除第一个元素，所以问题转化为有多少个序列存在一个非平凡的删除方式。进一步，我们可以发现，如果存在一个 2≤j≤i2\le j\le i 使得 aia_i 与 jj 互质，则一定存在一个非平凡的删除方式：先取若干次第一个元素直到 aia_i 成为第 jj 位，然后取 aia_i，然后再取第一个元素直到取完。反之，如果对于每个 ii 都不存在一个 2≤j≤i2\le j\le i 使得 aia_i 与 jj 互质，则一定不存在非平凡的删除方式，证明显然。

我们可以反向考虑问题，考虑有多少种序列不存在非平凡的删除方式，则每位互相独立。我们只需要对于每个 ii，求出有多少种 1≤ai≤m1\le a_i\le m 满足它与任意 2≤j≤i2\le j\le i 都不互质，每位的答案乘起来即可。而一个数与任意 2≤j≤i2\le j\le i 都不互质又可以进一步转化为与任意 2≤j≤i,j is prime2\le j\le i,j\text{ is prime} 都不互质，即是所有 ≤i\le i 的质数的倍数，也即：是当前所有质数乘积的倍数。所以我们可以维护一个当前质数的乘积 nownow，每次更新，答案便乘上 m/nowm/now。由于我们求的是“不存在删除方式”的方案数，而需要求“存在”的方案数，所以真正的答案要用总方案数减去“不存在”的方案数。由于要求长度在 [1,n][1,n] 之间，每次扫到一个位就将总答案加上这个位数的答案即可。

By cxm1024

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=998244353;
bool isprime[300010];
void init() {
    int n=300010;
    for(int i=0;i<=n;i++)
        isprime[i]=1;
    isprime[0]=isprime[1]=0;
    for(int i=2;i<=n;i++) {
        if(!isprime[i]) continue;
        for(int j=i*i;j<=n;j+=i)
            isprime[j]=0;
    }
}
signed main() {
    init();
    int n,m;
    cin>>n>>m;
    int now=1,ans=1,ansans=0,mi=1;
    for(int i=1;i<=n;i++) {
        if(now<=m&&isprime[i]) now=now*i;
        (ans*=m/now%mod)%=mod;
        mi=mi*(m%mod)%mod;
        (ansans+=(mi-ans+mod)%mod)%=mod;
    }
    cout<<ansans<<endl;
    return 0;
}

E. Cactus Wall

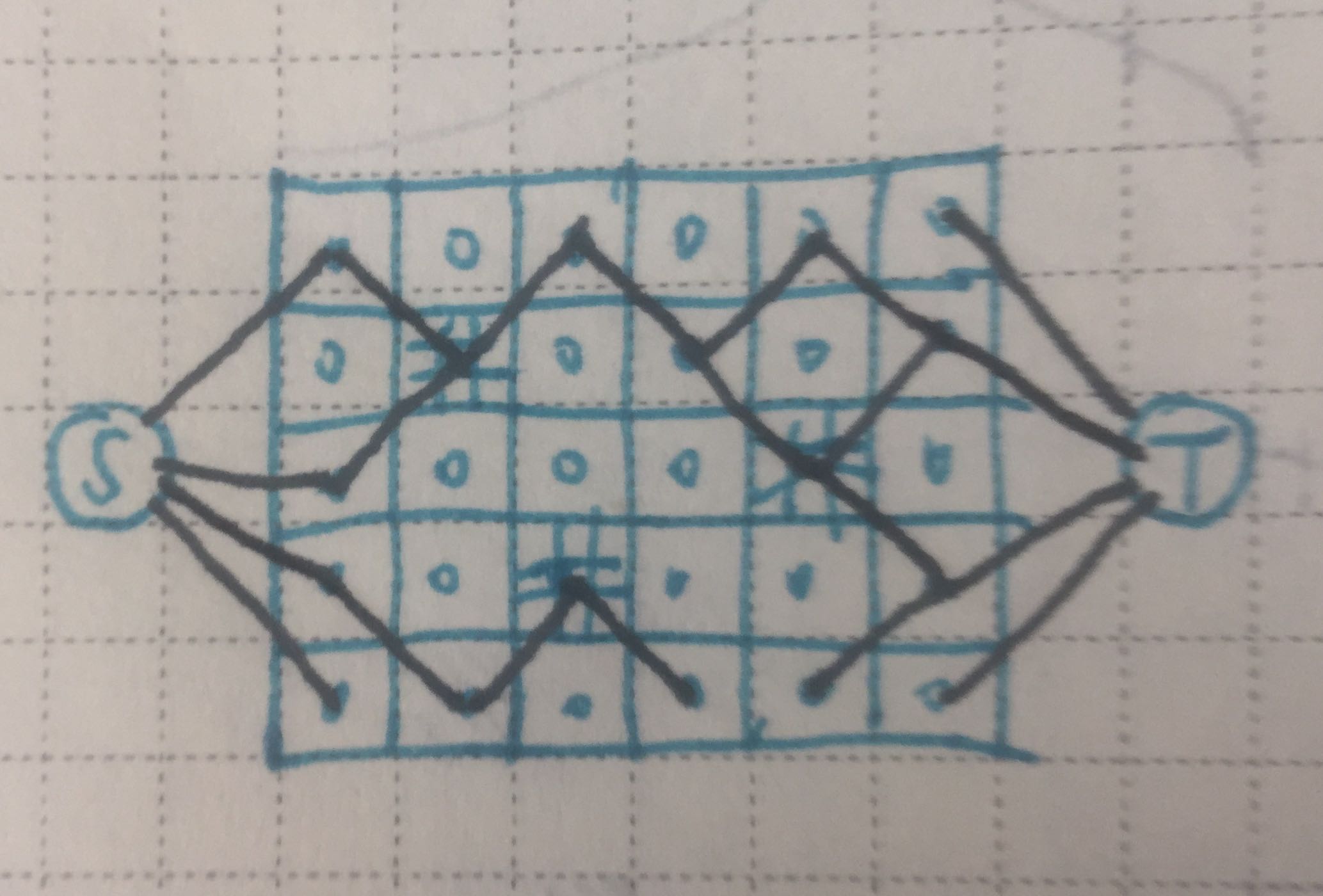
题意：有一个 n×mn\times m 的矩阵，有些位置是有障碍的。你需要添加尽可能少的障碍，满足障碍之间不能边相邻（但可以角相邻，保证初始矩阵满足条件），使得第一行到最后一行不存在路径（不连通）。

我们发现，最终的墙一定是由若干个对角相邻的障碍连起来的。我们可以预处理哪些位置不能放障碍（即与已有障碍相邻的位置），然后预处理这个障碍可以与哪些位置在答案的墙中相邻（即建图），然后问题转化为从第一列到最后一列建一个墙（路径）使得添加的障碍数尽可能少（最短路）。我们可以建一个虚点作为源点连向第一列的所有能放障碍的点，并建一个虚点作为汇点连着最后一列的点，跑一遍 BFS/Dijkstra 即可。

By SSRS_

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
#include <bits/stdc++.h>
using namespace std;
vector<int> dx = {1, 0, -1, 0};
vector<int> dy = {0, 1, 0, -1};
vector<int> dx2 = {1, 1, -1, -1};
vector<int> dy2 = {1, -1, 1, -1};
const int INF = 100000000;
int main(){
  ios::sync_with_stdio(false);
  cin.tie(nullptr);
  int t;
  cin >> t;
  for (int i = 0; i < t; i++){
    int n, m;
    cin >> n >> m;
    vector<string> s(n);
    for (int j = 0; j < n; j++){
      cin >> s[j];
    }
    vector<vector<bool>> ok(n, vector<bool>(m, true));
    for (int j = 0; j < n; j++){
      for (int k = 0; k < m; k++){
        if (s[j][k] == '#'){
          ok[j][k] = false;
          for (int l = 0; l < 4; l++){
            int x = j + dx[l];
            int y = k + dy[l];
            if (0 <= x && x < n && 0 <= y && y < m){
              ok[x][y] = false;
            }
          }
        }
      }
    }
    vector<vector<int>> d(n, vector<int>(m, INF));
    vector<vector<pair<int, int>>> pr(n, vector<pair<int, int>>(m));
    deque<tuple<int, int, int>> dq;
    for (int j = 0; j < n; j++){
      if (s[j][0] == '#'){
        d[j][0] = 0;
        dq.push_front(make_tuple(0, j, 0));
      } else if (ok[j][0]){
        d[j][0] = 1;
        dq.push_back(make_tuple(1, j, 0));
      }
    }
    while (!dq.empty()){
      int c = get<0>(dq.front());
      int x = get<1>(dq.front());
      int y = get<2>(dq.front());
      dq.pop_front();
      if (d[x][y] == c){
        for (int j = 0; j < 4; j++){
          int x2 = x + dx2[j];
          int y2 = y + dy2[j];
          if (0 <= x2 && x2 < n && 0 <= y2 && y2 < m){
            if (s[x2][y2]  == '#'){
              if (d[x2][y2] > d[x][y]){
                d[x2][y2] = d[x][y];
                pr[x2][y2] = make_pair(x, y);
                dq.push_front(make_tuple(c, x2, y2));
              }
            }
            if (ok[x2][y2]){
              if (d[x2][y2] > d[x][y] + 1){
                d[x2][y2] = d[x][y] + 1;
                pr[x2][y2] = make_pair(x, y);
                dq.push_back(make_tuple(c + 1, x2, y2));
              }
            }
          }
        }
      }
    }
    int mn = INF, p = -1;
    for (int j = 0; j < n; j++){
      if (d[j][m - 1] < mn){
        mn = d[j][m - 1];
        p = j;
      }
    }
    if (p == -1){
      cout << "NO" << "\n";
    } else {
      vector<string> ans = s;
      int x = p, y = m - 1;
      int CNT = 0;
      while (true){
        ans[x][y] = '#';
        if (y == 0){
          break;
        }
        int x2 = pr[x][y].first;
        int y2 = pr[x][y].second;
        x = x2;
        y = y2;
      }
      cout << "YES" << "\n";
      for (int j = 0; j < n; j++){
        cout << ans[j] << "\n";
      }
    }

  }
}