ABC-268解题报告

比赛传送门

D. Unique Username

题目传送门

暴搜即可，复杂度 $O(能过)$

E. Chinese Restaurant (Three-Star Version)

题目传送门

个人感觉非常好的一道题。

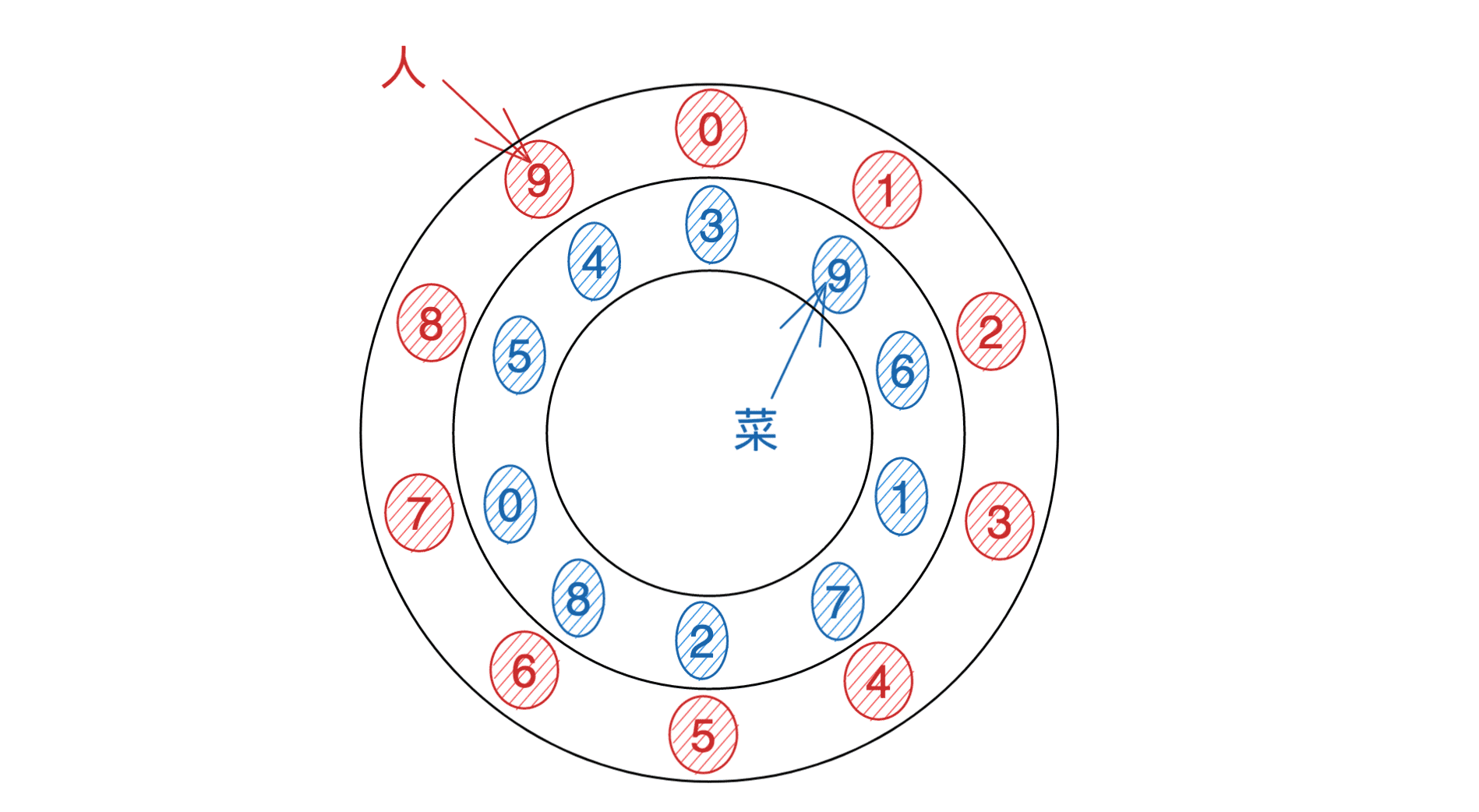
首先抽象一下题意：$n$ 个人和 $n$ 道菜分别呈环状排列，如下图：

环形可以旋转，若一个人与和他编号相同的菜距离为 $x$，会产生 $x$ 的贡献，问最小贡献和。

可以发现，有一些人用顺时针计算距离（如上图中的 $5$），其他人用逆时针计算距离（如 $3$）。设编号为 $i$ 的菜位于 $a_i$ ，我们预处理一个桶 $t_x$ 表示 $a_i-i=x$ 的个数。这样，用顺时针计算距离的人数可以得到，为 $t_1+t_2+\cdots+t_{n/2}$（钦定 $t_0$ 为逆时针计算、$t_{n/2}$ 为顺时针计算，便于后面转移）。若我们当前旋转了 $y$ 格，则此时用顺时针计算距离的人数为 $t_{y+1}+t_{y+2}+\cdots+t_{y+n/2}$。于是可以使用前缀和来优化这个步骤。为了让每一个 $y$ 都能正确地求得结果，我们将数组复制两遍（拆环为链）再求前缀和。

计算人数的用处是什么呢？是转移。考虑一次也不转的情况下，贡献和可以暴力预处理出来。每当顺时针转一格，用顺时针计算距离的人的贡献会 $-1$，而用逆时针计算距离的人的贡献会 $+1$，那么总贡献会减去顺时针的人数，再加上逆时针的人数。每次转移都用当前人数更新一下，即可 $O(1)$ 从 $y-1$ 的答案转移到 $y$ 的答案，每次转移后更新当前最优解。

细节：$n$ 为奇数和偶数的转移有细微差别，判断一下即可。

code:

#include<bits/stdc++.h>
using namespace std;
#define int long long
int a[200010],t[400010],s[400010];
signed main() {
    int n,ans=0,maxn;
    cin>>n;
    for(int i=0;i<n;i++) {
        cin>>a[i];
        ans+=min((a[i]-i+n)%n,(i-a[i]+n)%n);//暴力计算初始答案
        t[(a[i]-i+n)%n]++,t[(a[i]-i+n)%n+n]++;//t数组复制两遍，拆环为链
    }
    for(int j=1;j<n+n;j++)
        s[j]=s[j-1]+t[j];//前缀和
    maxn=ans;//ans为当前答案，maxn为当前最优解
    for(int i=1;i<n;i++) {//转i格后的答案
        ans-=s[i+n/2-1]-s[i-1];//减顺时针
        ans+=n-(s[i+n/2-1]-s[i-1]);//加逆时针
        if(n%2) ans-=t[i+n/2];//特殊处理n为奇数的情况
        maxn=min(maxn,ans);
    }
    cout<<maxn<<endl;
    return 0;
}

F. Best Concatenation

题目传送门

每个字符串内部的贡献是永远不变的，于是预处理。之后，每个字符串的有用信息仅剩 “x 的数量 $numx$”和“字符串的数字和 $sum$”。

考虑相邻两个串什么时候需要交换。设它们为 $s_i,s_{i+1}$，很容易发现，交换后只会影响它们之间的贡献，不会影响外部的贡献，所以只计算这两个之间的。

若不交换，贡献为 $numx_i\times sum_{i+1}$；若交换，贡献为 $numx_{i+1}\times sum_i$。要最大化贡献值，则依此排序即可。

code:

#include<bits/stdc++.h>
using namespace std;
#define int long long
struct node {
    int numx,sum;
}a[200010];
signed main() {
    int n,ans=0;
    cin>>n;
    for(int i=1;i<=n;i++) {
        string s;
        cin>>s;
        int now=0;
        for(int j=s.size()-1;j>=0;j--)
            if(s[j]=='X') ans+=now,a[i].numx++;
            else now+=s[j]-'0',a[i].sum+=s[j]-'0';
    }
    sort(a+1,a+n+1,[](node p,node q) {
        return p.numx*q.sum>q.numx*p.sum;
    });
    int now=0;
    for(int i=n;i>=1;i--)
        ans+=a[i].numx*now,now+=a[i].sum;
    cout<<ans<<endl;
    return 0;
}