ARC-138解题报告

发表于 更新于 分类于

比赛传送门

A. Larger Score

因为只需要增加而不限制增加量，所以找到一对前小后大的数对，设法将它们交换即可。具体来说，所以对于 k+1k+1 到 nn 的一个位置 ii，找到在前 kk 个当中离它最近的（最后的）、比它小的位置 jj（取后缀 min⁡\min 后用 lower_bound 找出），用 k−jk-j 次操作将 jj 移到位置 kk，用 i−k−1i-k-1 次操作将 ii 移到位置 k+1k+1，再用一次操作交换即可，总操作数为 (k−j)+(i−k−1)+1=i−j(k-j)+(i-k-1)+1=i-j 次。这就是一个位置的答案。计算每个位置的答案，取最小值即可。

code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<bits/stdc++.h>
using namespace std;
int a[400010];
int main() {
    int n,k,ans=1e9;
    cin>>n>>k;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    for(int i=k-1;i>0;i--)
        a[i]=min(a[i],a[i+1]);
    for(int i=k+1;i<=n;i++) {
        int tmp=lower_bound(a+1,a+k+1,a[i])-a-1;
        if(tmp==0) continue;
        ans=min(ans,i-tmp);
    }
    if(ans==1e9) cout<<-1<<endl;
    else cout<<ans<<endl;
    return 0;
}

B. 01 Generation

由于只有前面加1反转和后面加0两种操作，所以考虑它们的分界线。

在前面的部分全部由添加1反转构成，所以一定是 010101... 这种形式，找出最长的满足要求的前缀，这就是第一部分。第一部分的0必须依次插入，可以发现，每插入一个0，第二部分就会受到影响，得到反转，所以当在第二部分中遇到连续的若干个0或连续的1的时候，它们一定（在最优解中）是同一块插入的。

而两块0、1的交界处必然进行了一次一操作（最优解中）。这样只需要比较操作一的次数（即最长01前缀的长度）和操作二的变化次数即可。如果操作一的次数小于第二部分的变化次数则不可行，反之可行。

这道题还有另一种思考方式，即倒序思考，将插入操作转化为删除。读者可自行考虑。

code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<bits/stdc++.h>
using namespace std;
bool a[200010];
int main() {
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    if(a[1]==1) {
        cout<<"No"<<endl;
        return 0;
    }
    int now=1;
    while(now<n&&a[now]!=a[now+1]) now++;
    if(now==n) {
        cout<<"Yes"<<endl;
        return 0;
    }
    int ans=a[n];
    for(int i=n-1;i>now;i--)
        if(a[i]!=a[i+1]) ans++;
    if(ans<=now) cout<<"Yes"<<endl;
    else cout<<"No"<<endl;
    return 0;
}

C. Rotate and Play Game

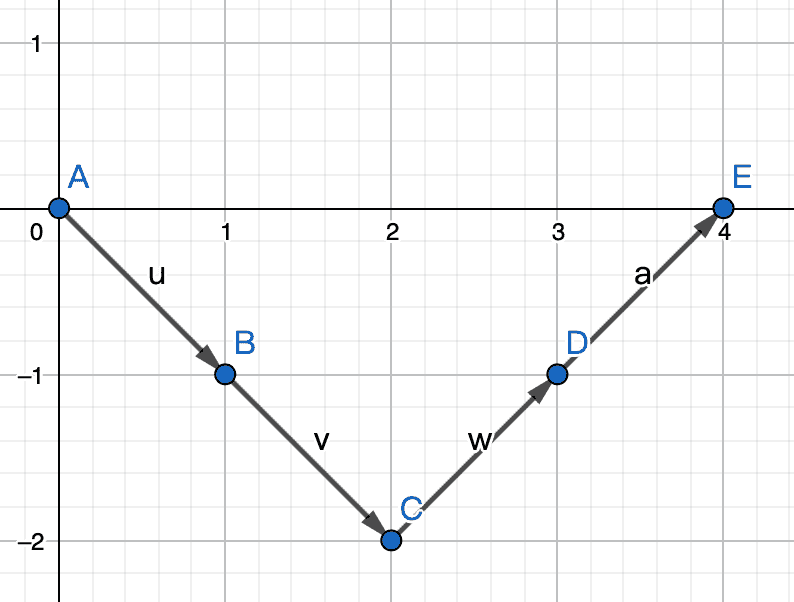
题目问最好情况，那么有一个很自然的猜测：最好情况一定可以取得最优解，即拿走大的那一半，留下小的那一半。这就要求我们在翻转之后，在任何一个前缀当中，小的数的个数 ≥\ge 大的数的个数（这样才能保证对方走到大的数之前，我已经把它拿掉了）。设较小的一半数为 +1+1，较大的一半为 −1-1，则相当于要求前缀和中不存在负数。在坐标系中表现出来就是这样的：

（数据 3 4 1 2 的图像）

那么，分成两半后互换就可以表示为，选一个点，以它为原点开始，再走回自己结束。这样结论就很显然了：选最低的点，以它为起点，坐标为0，那么之后无论怎么走也不会比它更低，满足要求。在此例子中，选择点 CC 为起点，这样答案序列为 1 2 3 4，满足要求。

（不得不说是一道非常巧妙的转化题）

code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<bits/stdc++.h>
using namespace std;
int a[200010],b[200010];
int main() {
    int n;
    cin>>n;
    for(int i=1;i<=n;i++) {
        cin>>a[i];
        b[i]=a[i];
    }
    sort(b+1,b+n+1);
    int fen=b[n/2];
    long long mini=0,ans=0;
    for(int i=n/2+1;i<=n;i++)
        ans+=b[i];
    for(int i=1;i<=n;i++)
        if(a[i]<=fen) a[i]=1;
        else a[i]=-1;
    for(int i=2;i<=n;i++)
        a[i]+=a[i-1];
    for(int i=2;i<=n;i++)
        if(a[i]<a[mini])
            mini=i;
    cout<<mini<<" "<<ans<<endl;
    return 0;
}