勾股定理证明

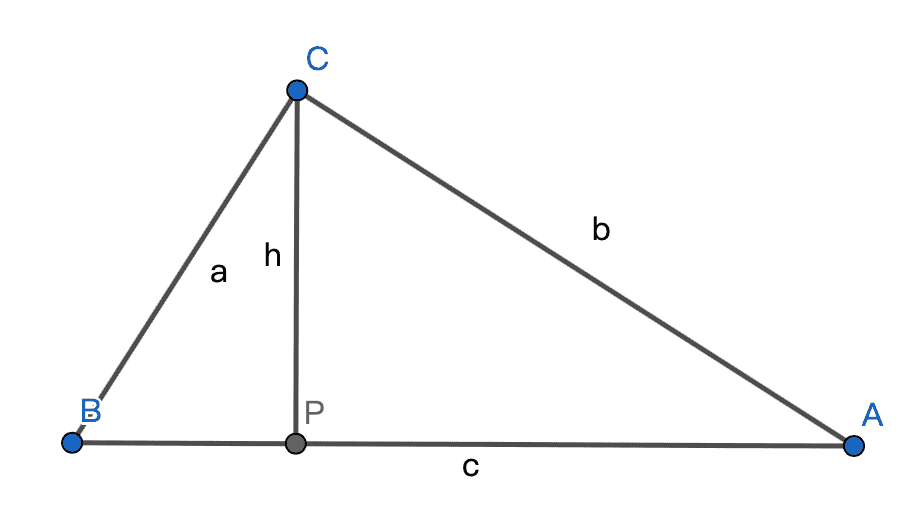
在这个直角三角形中，我们设以 $c$ 为底的大三角形面积为 $S_c$，以 $a,b$ 为底的两个小三角形的面积分别为 $S_a,S_b$。

显然，$S_c=\frac{ch}{2}=c^2\cdot\frac{h}{2c}$。令 $m=\frac{h}{2c}$，则有 $S_c=mc^2$。

同理，$S_a=a^2\cdot\frac{h_a}{2a}$（其中 $h_a$ 表示三角形 $BPC$ 中以 $a$ 为底的高）。显然该三角形与大三角形 $ABC$ 相似，所以 $\frac{ha}{h}=\frac{a}{c}$，即 $\frac{h_a}{2a}=\frac{h}{2c}=m$，所以 $S_a=ma^2$。同理 $S_b=mb^2$。

又因为，$S_c=S_a+S_b$，所以 $mc^2=ma^2+mb^2$，即 $c^2=a^2+b^2$。