CFR-755-Div.2解题报告

比赛传送门

赛时AC三道，补题做出一道。

A. Mathematical Addition

Problem

给你两个正整数 $u,v$，求一对合法的 $x,y$ 使得 $\frac{x}{u}+\frac{y}{v}=\frac{x+y}{u+v}$。

解方程。

$$\begin{array}{c} \frac{vx+uy}{uv}=\frac{x+y}{u+v} \\ (vx+uy)(u+v)=uv(x+y) \\ uvx+u^2y+v^2x+uvy=uvx+uvy \\ u^2y+v^2x=0 \end{array}$$

则显然一组合法解为 $\begin{cases}x=-u^2\\y=v^2\end{cases}$

B. Coloring Rectangles

Problem

有一个 $n\times m$ 的矩阵，每个方格均为红色。你可以任意多次的横切或纵切（必须贯穿整块），不能出现 $1\times 1$ 的矩阵，问切完后最少需要涂几个蓝色格子才能使得红色格子不相邻。

example: $2\times 5$

• Solution 1
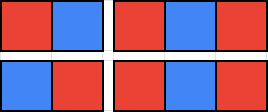
• Solution 2

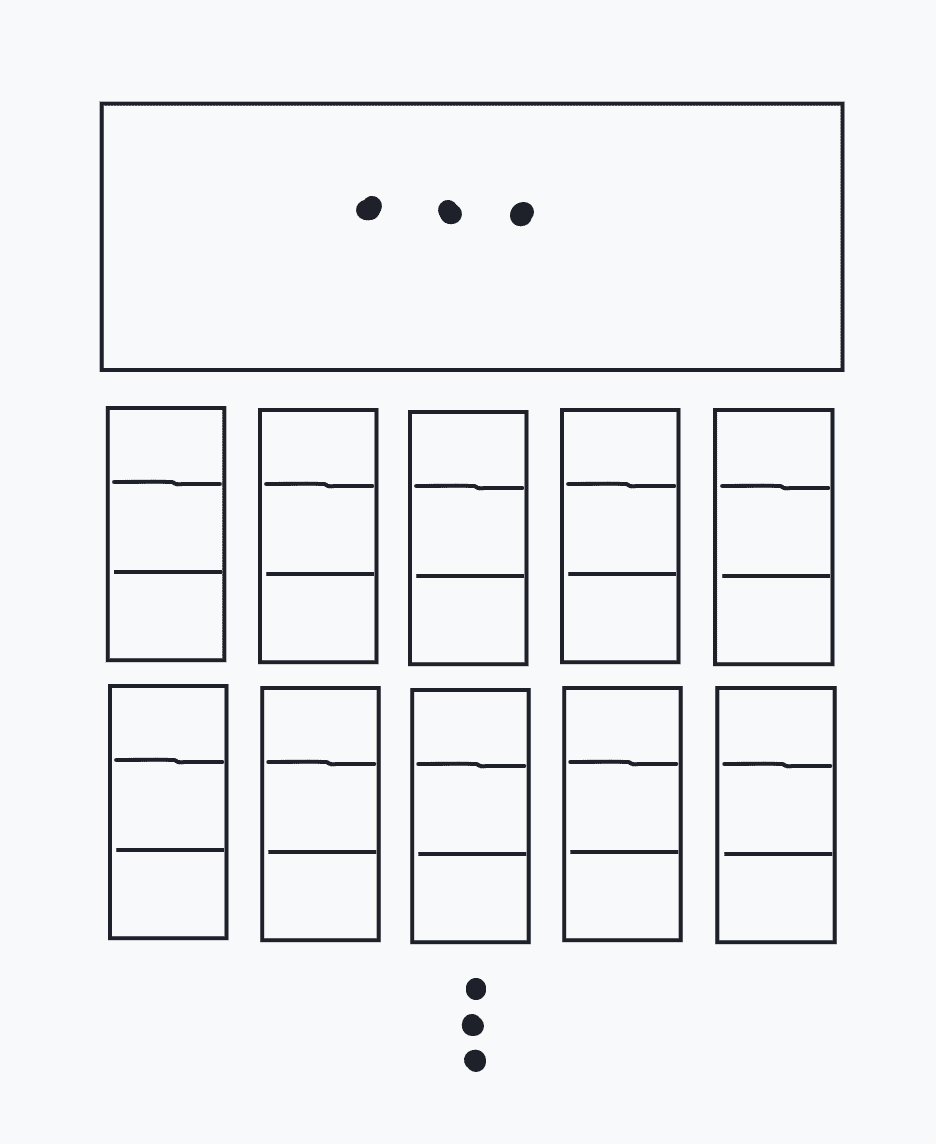
容易发现，把格子割成 $1\times 3$ 是最优的，于是考虑在不对后续操作产生影响的前提下，把它切成这样：

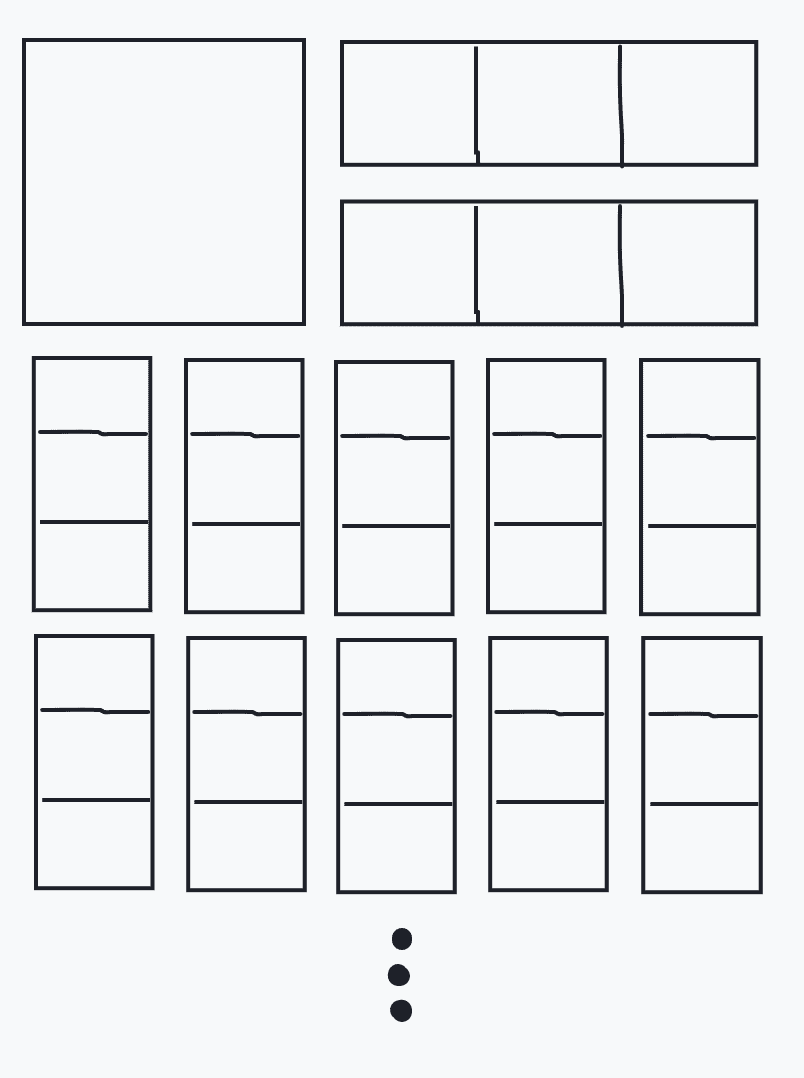
然后再切成这样：

最后特判剩下的。注意切的时候要时刻堤防剩下一行或剩下一列的情况，防止出现 $1\times 1$。

通过找规律，我们可以发现，答案为 $\lceil\frac{n\times m}{3}\rceil$。

C. Two Arrays

Problem

给你两个数组 $a,b$，问能否通过把 $a$ 进行一次变换得到 $b$。

变换方式：在 $a$ 数组中选出若干个数分别 $+1$，然后随意排列顺序。

大水题。$a,b$ 分别排序，看是否每个 $a$ 数组的元素都等于 $b$ 的对应元素或等于 $b$ 的对应元素 $+1$。

D. Guess the Permutation

Problem

这是一道交互题。

有一个初始数组 $a$，满足 $a_i=i$，即 ${1,2,3...}$。现在有 $1<=i<j<=k<=n$，将 $[i,j-1],[j,k]$ 分别翻转。你需要通过不超过 $40$ 次询问得到 $i,j,k$ 的值。

每一次询问你可以给出 $l,r$，得到 $[l,r]$ 中的逆序对个数。

$n\le 10^9(\log_2(10^9)\approx 30)$

1. 用一次 $\log$ 找到 $k$：二分 $mid$，询问 $[mid,r]$ 中逆序对个数，如果不为 $0$，则 $k$ 在 $[mid+1,r]$ 中，否则在 $[l,mid]$ 中。
2. 用两次询问 $[1,k]$ 和 $[1,k-1]$ 来获得 $j$ 的位置：一段降序区间 $[l,r]$ 的逆序对数减去 $[l,r-1]$ 的逆序对数等于 $len-1$，于是 $[1,k]-[1,k-1]=len_{[j,k]}-1$（$j$ 前面的都被抵消了），用 $k-(len-1)$ 即可求出 $j$。
3. 同理用两次询问 $[1,j-1]$ 和 $[1,j-2]$ 来获得 $i$ 的位置。

询问次数约为 $\log(n)+4$。

不开 long long 见祖宗（逆序对个数最多有 $n^2$ 级别）。