本篇题解献给和我一样看不懂其他题解的状压DP小白
相信大家都是看了其他题解看不懂才看到这篇题解的(莫名自信),所以什么每行棋子数递减啊,每行的棋子都排在左边啊,就不用我多说了,直接切入正题(大段文字多,请耐心观看)。
轮廓线DP
没见过不用慌,我也没见过(雾
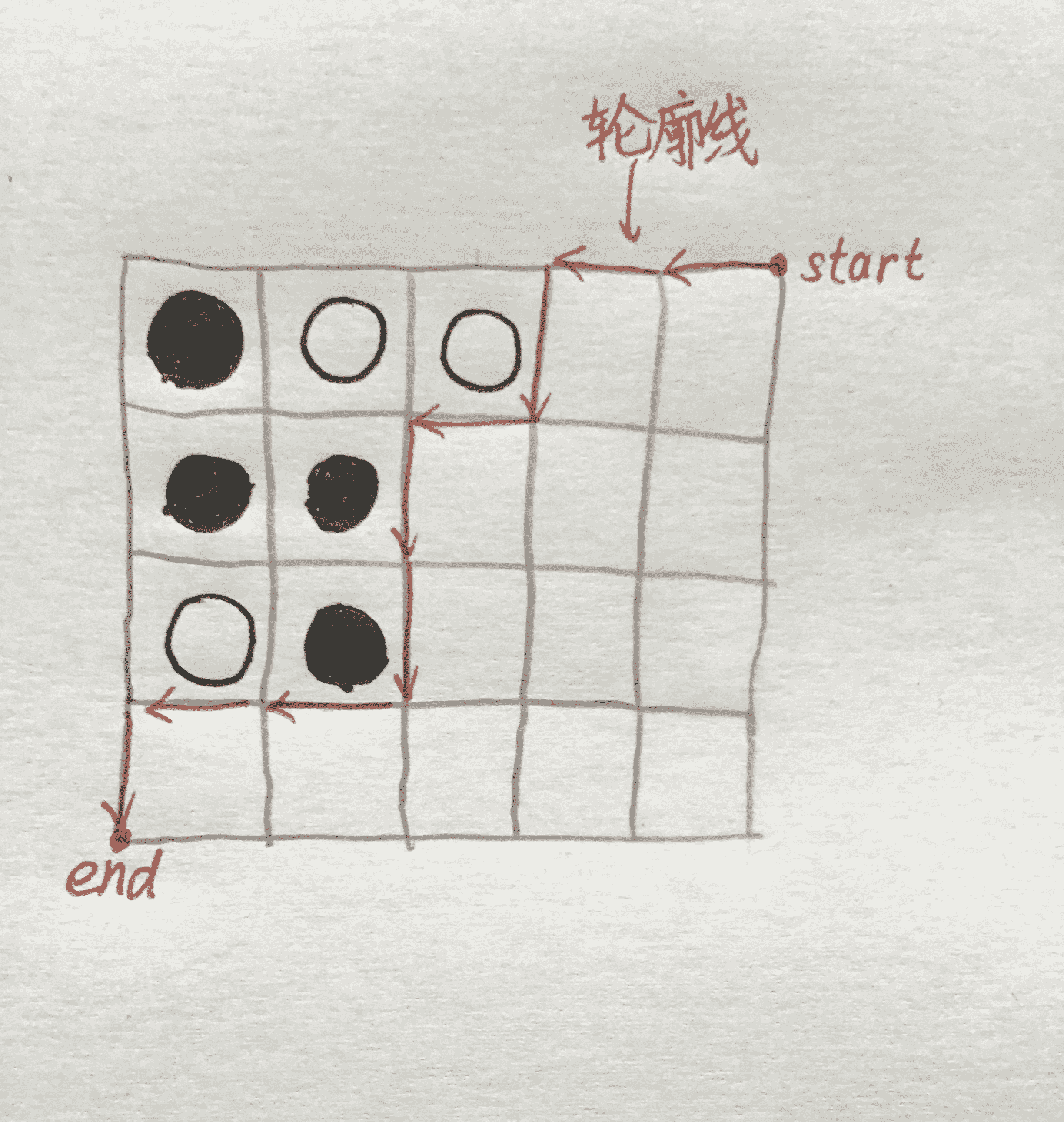
轮廓线,就是把矩阵从右上角到左下角沿着有棋子和没棋子的分界线描一下,往下走就用1表示,往左走就用0表示。这样我们就得到了一个01串,即一个二进制数,这就是我们的DP状态。
例如(图丑勿喷)
![]()
这种情况下轮廓线状态为左左下左下下左左下,即001011001(2)=89
我们设f[s](s就是轮廓线状态)表示从轮廓线表示的局面一直下到最终下满的过程中“先手-后手”最大是多少。我们可以发现,只根据s就可以知道已经下了那些棋,但不能知道具体是黑棋还是白棋,然而根据f的定义,f[s]的值和前面怎么下的没有关系,它只管之后怎么下,所以我们只用一维轮廓线就OK,不需要记录之前怎么下的。
那么状态有了,怎么转移呢?以上图为例,即将要白棋(后手)下棋,后手肯定希望他下的一步棋能使得从现在开始(以前的我们不管)先手-后手得分尽可能小(如果是负数那他更开心了),所以f[s]=所有再下一步棋可能得到的方案s′minf[s′]−b[x][y](x,y就是即将下的那一步棋的坐标)。
同理,如果即将先手下,就把上面的式子里min改成max(因为他希望下这步棋能使得他的得分-对方的得分最大),−b[x][y]改成+a[x][y]。
这样我们就可以用记忆化搜索很容易地跑出来了。
哎等等,我们还有两个问题没解决,观察上面的式子,我们还不知道怎么枚举“所有再下一步棋可能得到的方案s′”,也不知道怎么根据轮廓线的变化找出具体坐标x和y啊?
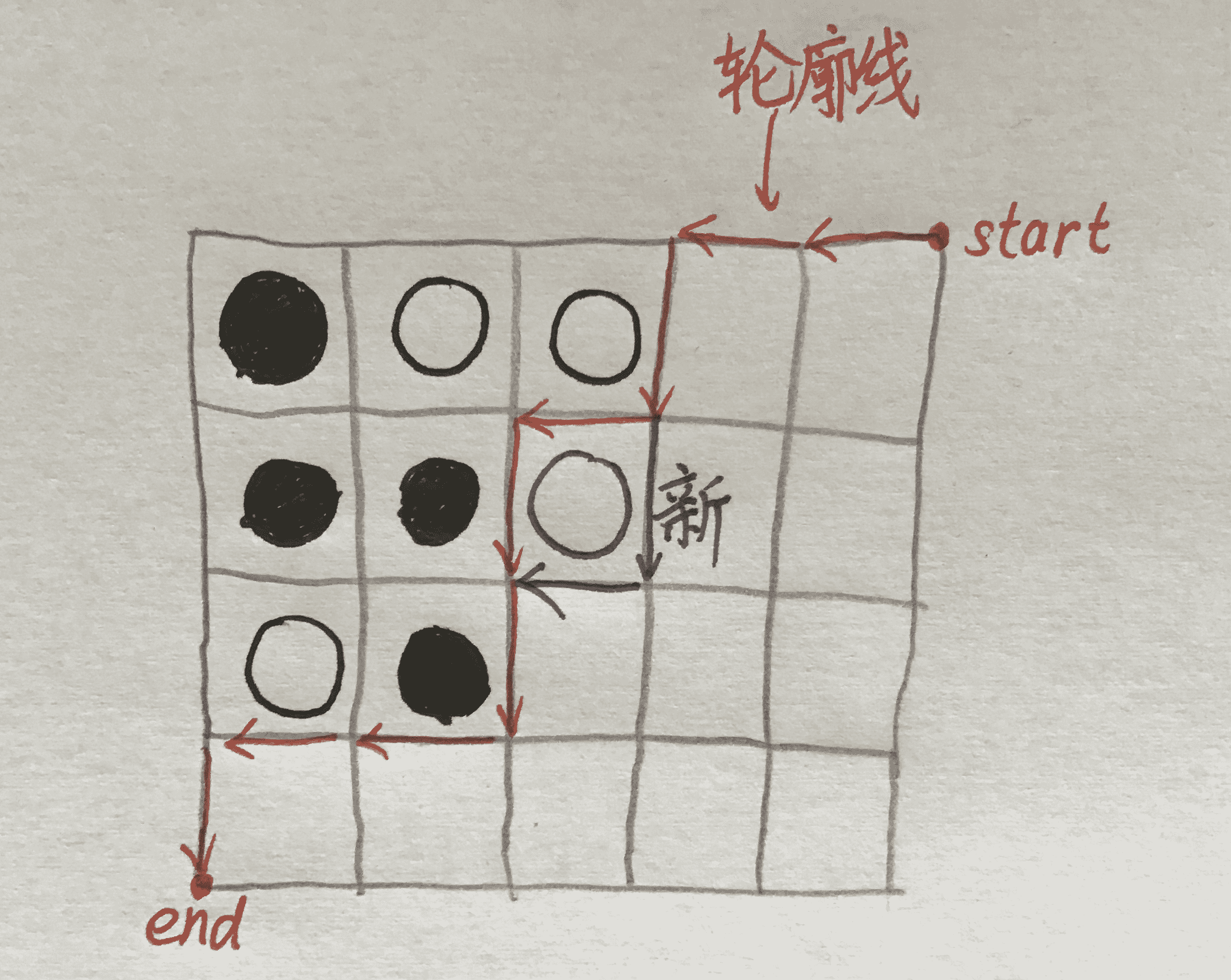
我们一个一个解决,先看第一个问题。还是以上图为例,白棋(后手)可以下在(1,4),(2,3),(4,1)三个位置,但转移的时候电脑只知道当前的轮廓线,所以我们需要找这三个点的共同特点,那就是处在轮廓线左和下的拐角处,也就是轮廓线中先出现一个0,再出现一个1。现在我们知道了轮廓线上放棋子的位置,怎么得出放棋子后的轮廓线状态呢?我们还是以上图为例,如果我们放在(2,3)处,进行一个对比。
原:001011001(2)
新:001101001(2)
![]()
我们发现只有第四位和第五位变了,而原先的第四位和第五位就是我们之前说的先出现一个0,再出现一个1,那么转移就是把0变成1,把1变成0。
具体来说,就是当我们枚举到一个i,使得原状态的(从低位数)第i位是1,第i+1位是0,那么就把状态异或上3<<i(可以对照例子手推一下)。
开始讨论第二个问题,我们知道该在轮廓线的哪一位上下棋,怎么知道那步棋的具体坐标呢?这个问题比较容易解决,只需要在枚举i时维护当前看到哪个坐标即可(详见代码)。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| #include<iostream>
using namespace std;
int n,m;
int a[20][20],b[20][20];
int f[1048580];
bool vis[1048580];
int dfs(int s,bool now)
{
if(vis[s])
return f[s];
vis[s]=1;
if(s==(1<<(n+m))-(1<<m))
return 0;
int num0=0,num1=0;
if(now)
{
f[s]=-2147483647;
for(int i=0;i<n+m-1;i++)
{
num1+=((s&(1<<i))>>i);
num0+=(!((s&(1<<i))>>i));
if((s&(1<<i))>0&&(s&(1<<(i+1)))==0)
f[s]=max(f[s],dfs(s^(3<<i),0)+a[n-num1+1][num0+1]);
}
return f[s];
}
else
{
f[s]=2147483647;
for(int i=0;i<n+m-1;i++)
{
num1+=((s&(1<<i))>>i);
num0+=(!((s&(1<<i))>>i));
if((s&(1<<i))&&!(s&(1<<(i+1))))
f[s]=min(f[s],dfs(s^(3<<i),1)-b[n-num1+1][num0+1]);
}
return f[s];
}
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>a[i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>b[i][j];
cout<<dfs((1<<n)-1,1)<<endl;
return 0;
}
|